همه چیز درباره فیثاغورس: زندگی شخصی تا کاربردهای قضیه فیثاغورس

زندگینامه فیثاغورس

تولد و دوران کودکی

فیثاغورس حدود 565 سال پیش از میلاد در جزیره یونانی ساموس، واقع در دریای اژه شرقی، متولد شد. او در یک محیط فرهنگی غنی و در دوران طلایی یونان پرورش یافت. برخی محققان بر این باورند که او پسر قلم‌زنی محلی و ثروتمند به نام منسارخوس بود، اما در منابع دیگری او را پسر آپولو، الهه‌ی شعر و موسیقی یونان باستان، دانسته‌اند.

پیش از تولد او، منطقه‌ی ساموس به دلیل سفرهای تجارتی و سیاحتی به یکی از ثروتمندترین جزیره‌های اژه تبدیل شده بود. این ثروت و رونق اقتصادی، ساموس را به رقیبی تجاری برای کشورهایی چون مصر و اسپانیا تبدیل کرد و زمینه‌های رشد علمی و فرهنگی آن فراهم شد.

دوران جوانی و تحصیلات

فیثاغورس در دوران طلایی یونان متولد شد و در این محیط رشد کرد. با این حال، اطلاعات کمی از زندگی شخصی او وجود دارد و این‌که پدر و مادرش چگونه بودند و او چه ارتباطی با آن‌ها داشت، مشخص نیست. برخی نکات قابل توجه در این زمینه عبارتند از:

• فقدان اطلاعات شخصی: متأسفانه، بسیاری از جزئیات زندگی او در دوران کودکی ناشناخته مانده است.
• تأثیر خانواده: نشانه‌هایی از فقدان زندگی خانوادگی در او مشهود است، چنان‌که فیلسوفانی چون افلاطون، دکارت و نیچه نیز از خانواده‌ی خوبی برخوردار نبودند.

پس از رسیدن به سن جوانی، فیثاغورس برای یادگیری دانش ریاضی به مصر رفت. در آن دوران، افراد زیادی برای کسب علم و دانش به شرق مهاجرت می‌کردند و مصر به عنوان کشوری پیشرفته از لحاظ فرهنگ و علوم مختلف شناخته می‌شد.

گفته می‌شود فیثاغورس چند سال بعد از مصر به بابل سفر کرد و متوجه شد که ریاضیدانان بابل در محاسبات ذهنی پیشرفت‌هایی دارند که فراتر از درک مصری‌ها است. همچنین، بر اساس برخی منابع، او با موبدان ایرانی و برهمن‌های هندی نیز در مسیر بابل و سایر کشورهای شرقی روبرو شده بود.

بازگشت به ساموس و فعالیت‌های علمی

فیثاغورس پس از چند سال تحصیل و سفر به ساموس بازگشت. در این زمان، پلی کرات، شخصی باهوش و زیرک، فرمانروا شده بود. او با گسترش بازرگانی و تجارت‌های دریایی درآمد لازم برای ساخت بناهای عظیم را فراهم کرد و به دعوت دانشمندان و هنرمندان از سراسر اژه پرداخت.

فیثاغورس که دانشمند و عالمی بزرگ بود، تبدیل به یکی از شخصیت‌های برجسته‌ای شد که حتی در سیاست و مسائل حکومتی مداخله می‌کرد.

کشف قضیه فیثاغورس

در سال‌های ابتدایی اقامت فیثاغورس در کرتون، او اقدامات زیادی در زمینه ریاضیات انجام داد. یکی از این اقدامات، کشف قضیه‌ی مهم فیثاغورس بود. نکات کلیدی درباره این کشف شامل موارد زیر است:

• عدم وجود نوشته‌های شخصی: از آن‌جا که او نوشته‌ای از خود به یادگار نگذاشت، مدرکی وجود ندارد که چگونه قضیه‌اش را ابداع و اثبات کرد.
• آثار مریدان: با این حال، مریدان او آثاری نوشتند که برای شناخت بیشتر فیثاغورس قابل استناد است.
• کشفیات شگفت‌انگیز: کشف قضیه‌ی فیثاغورث موفقیت‌آمیز بود و به تعدادی کشفیات شگفت‌انگیز درباره مثلث قائم‌الزاویه با اضلاع انتگرالی (یا اعداد صحیح) منجر شد.

کشفیات ستاره‌شناسی و موسیقی سیارات

بررسی‌های فیثاغورس جان تازه‌ای به مباحث ریاضی بخشید. برای او، ریاضیات چیزی فراتر از یک کار عقلانی بود، زیرا می‌خواست با آن جهان را توضیح دهد. نکات زیر به وضوح نشان‌دهنده این دیدگاه است:

• ضرایب و ویژگی‌های اعداد: او اعتقاد داشت که ضرایب و ویژگی‌های اعداد، سادگی و اشکال آن‌ها نشان از ماهیتی حقیقی دارد که بر همه‌چیز حکمفرماست.
• تأثیر بابلی‌ها: این موارد در مطالعات ستاره‌شناسی فیثاغورس نیز وجود داشت. او تحت تأثیر بابلی‌ها و فردی به نام آناکسیمندر بود که برای اولین بار نقشه‌ی آسمان‌ها را رسم کرد.

فیثاغورس همچنین عقیده داشت که حرکت ادواری اجسام فضایی به عقاید او در باب ریاضی و نجوم تحکیم بخشیده است. او از همان ابتدا بر این باور بود که زمین در مرکز عالم قرار دارد و مشاهدات او نشان داد که هر کدام از سیارات در فاصله‌ی معینی از یکدیگر قرار دارند. او این وضعیت را به هشته‌ی موسیقی تشبیه کرد و بر این اساس، سیارات نوعی هارمونی آسمانی تولید می‌کنند که به موسیقی کرات معروف است.

فیثاغورس معتقد بود که به علت عادت انسان‌ها به این موسیقی از ابتدای خلقت، نمی‌توان آن را شنید.

تبعید و زندگی در کرتون

با توجه به وضعیت سیاسی و دیپلماتیک منطقه‌ی ساموس، فیثاغورس به برتری خود در میان حاکمان و درباریان اصرار ورزید که در نهایت منجر به اخراج او از ساموس شد. براساس افسانه‌ای تاریخی، او به زندانی در جنوب جزیره منتقل شد. در سال 529 پیش از میلاد، او به مگناگراسیا سفر کرد و در کرتون که مستعمره‌ی یونان بود، اقامت گزید. در این زمان، او خود را فیلسوف می‌دانست و به واسطه‌ی همین عنوان، شاگردان و افراد زیادی را دور خود جمع کرد.

تأثیرات و عقاید فیثاغورس

فیثاغورس و شاگردانش مخالف اصول حکومت دموکراسی بودند و بارها با آزار و اذیت پیروان آن روبرو شدند. چنان‌که گفته می‌شود مدرسه‌ی او توسط دموکراسی‌خواهان سوزانده شد و تعدادی از شاگردانش به قتل رسیدند. در برخی منابع آمده که در حال فرار از هجوم کسانی که قصد سوزاندن او را داشتند، مورد حمله قرار گرفت و به قتل رسید. مدارک معتبری برای اثبات این قضیه وجود ندارد و حتی محل دفن او مشخص نیست.

عقاید مذهبی و فلسفی

فیثاغورس عقاید خاصی در باب سیاست و اخلاقیات داشت. او در کرتون به عنوان یک معلم آغاز کرد و سپس به رهبر دینی تبدیل شد. دانشجویان او در ریاضی و فلسفه به پیروی از او پرداختند و گفته می‌شود در آن زمان حدود 300 نفر مرید داشت.

او اعتقاد داشت که “همه‌ چیز عدد است.” این اعتقاد به اصلی مهم در مذهب و عقاید او تبدیل شد که برای برخی باورپذیر و برای عده‌ای غیرقابل باور بود.

زندگی اجتماعی فیثاغورس و آداب و رسوم

اندیشه‌های فیثاغورس ترکیبی از ریاضی، عرفان، اخلاقیات و رژیم‌های غذایی بود. او و شاگردانش در خانه‌های اشتراکی سکونت داشتند و در همه‌چیز با هم شریک بودند. در این خانه‌ها، تبعیض طبقاتی، نژادی و جنسیتی وجود نداشت و با برده‌ها نیز مانند افراد عادی رفتار می‌شد. نکات کلیدی در این زمینه عبارتند از:

• زندگی مشترک: فیثاغورسیان در خانه‌های اشتراکی زندگی می‌کردند و در تمامی امور با یکدیگر شریک بودند.
• مبانی انسانی: آنان کم‌کم دین تازه‌ای بر مبنای انسانیت پایه‌گذاری کردند و حاکمان شهرهای یونان به حمایت از فلسفه‌ی فیثاغورس و شاگردان او پرداختند.

پایان زندگی و میراث فیثاغورس

در سال 450 پیش از میلاد، موجی از احساسات مردم‌سالاری شکل گرفت که منجر به شورش‌های مدنی شد. فیثاغورسی‌ها هدف عمومی قرار گرفتند و بسیاری از خانه‌های اشتراکی آن‌ها سوزانده شد. پس از این وقایع، جنبش فیثاغورسی‌ها به دو گروه تقسیم شد: یک گروه شامل جمعیت بزرگ مستمعین و دیگر گروه شامل ریاضیدانانی که به سرزمین اصلی یونان فرار کردند.

فیثاغورس حدود سی سال در کرتون زندگی کرد و در این مدت به مطالعات ریاضی و ستاره‌شناسی پرداخت. او در نهایت به عنوان یکی از بزرگترین اندیشمندان تاریخ، با کشفیات ریاضی، مذهبی و ستاره‌شناسی خود، جهان را متحول کرد. میراث او همچنان در دنیای علم و فلسفه باقی مانده و تأثیراتش بر نسل‌های آینده غیرقابل انکار است.

زندگی‌نامه دیگر افراد موفق: اگر به مطالعه زندگی‌نامه افراد موفق علاقه دارید توصیه می‌کنیم مقالات حسن خسروشاهی، شهرداد روحانی، دیپاک چوپرا و هایزنبرگ را در رسانۀ دانشگاه کسب و کار بخوانید.

اکتشافات و ابداعات فیثاغورس

1. اعداد کامل

فیثاغورس و پیروانش، تفکرات عمیق و پیچیده‌ای در مورد اعداد داشتند که ترکیبی از عرفان و ریاضیات بود. یکی از مهم‌ترین ابداعات او معرفی دو نوع عدد کامل بود:

• عدد کامل اول: عدد 10 که به این دلیل انتخاب شد که جمع چهار عدد اول (1، 2، 3 و 4) برابر با 10 است: 10=4+3+2+1 10 = 4 + 3 + 2 + 1
  • دستگاه چهارتایی: فیثاغورسیان این اعداد را دستگاه چهارتایی می‌نامیدند و در یک هرم جایگذاری می‌کردند.
  • مقدس بودن عدد 10: آن‌ها به عدد 10 قسم می‌خوردند و این عدد را مقدس می‌دانستند.
• عدد کامل دوم: اعدادی که با جمع فاکتورهای خود برابر می‌شدند، مانند عدد 6: 6=1+2+3 6 = 1 + 2 + 3

2. قضیه‌ی فیثاغورس

یکی از مهم‌ترین ابداعات فیثاغورس که نام او را جاودانه کرد، کشف قضیه‌ی فیثاغورس بود. این قضیه به شرح زیر است:

• تحقیق بر روی مثلث قائم‌الزاویه: فیثاغورس با تحقیق روی مثلث قائم‌الزاویه به این نتیجه رسید که مساحت مربعی که با وتر یک مثلث قائم‌الزاویه ساخته می‌شود، با مجموع مساحت دو مربعی که با اضلاع مجاور زاویه قائم ساخته می‌شوند، برابر است.
• بیان قضیه: در هر مثلث قائم‌الزاویه، مجذور وتر برابر با مجموع مجذور دو ضلع مجاور زاویه‌ی قائمه است. این قانون بعدها با عنوان قضیه‌ی فیثاغورس (یا فیثاغورث) مشهور شد.
• اثبات‌های متعدد: برای این قضیه، 400 اثبات شناخته‌شده توسط ریاضیدانان مختلف تدوین شده است.

این مقاله را هم بخوانید:  زندگی‌نامه کامل رنه دکارت پدر فلسفه مدرن + لیست آثار او

3. اشکال منتظم

در دوران زندگی فیثاغورس، تنها چهار شکل منظم شناخته شده بود:

• هرم سه‌وجهی
• هشت‌وجهی
• مکعب
• دوازده‌وجهی

فیثاغورس روش هندسی ساخت این چهار شکل منظم را کشف کرد و به این نتیجه رسید که:

• شکل دوازده‌وجهی: این شکل تقریباً شبیه به یک کره است که شامل دوازده پنج‌ضلعی منتظم می‌باشد و در حقیقت با شکل کلی جهان شباهت دارد.
• اسرار مرموز: این اسرار و حقایق بسیار مهم و مرموز بود. به گونه‌ای که وقتی یکی از اعضای گروه او، راز دوازده‌وجهی را برای سایر مردم فاش کرد، توسط افراد ناشناس کشته شد و در یک فاضلاب عمومی غرق گردید.

4. اعداد گنگ

تحقیقات و بررسی‌هایی که فیثاغورس بر نسبت اعداد انجام داد، منجر به کشف اعداد گنگ شد. نکات قابل توجه در این زمینه شامل موارد زیر است:

• عدم دانش در مورد اعداد گنگ: تا پیش از این، دانش چندانی درباره‌ی اعداد گنگی مانند رادیکال وجود نداشت و ساختمان ریاضی بر پایه‌ی اعداد صحیح بنا شده بود.
• اکتشاف اعداد گنگ: اکتشاف اعداد گنگ، یک برگ برنده برای فیثاغورسیان بود که نباید فاش می‌شد.
• هیپاسوس: مدتی بعد، فردی به نام هیپاسوس راز اعداد گنگ را برای دیگران آشکار کرد. این اقدام باعث شد که اعضای گروه برای او آرزوی مرگ کنند و سرانجام او در کشتی شکسته‌ای از بین رفت.

بررسی قضیه فیثاغورس و کاربردهای آن

قضیه فیثاغورس یکی از مهم‌ترین و بنیادی‌ترین قوانین در ریاضیات است که به نام فیثاغورس، ریاضیدان و فیلسوف یونانی قرن ششم پیش از میلاد، نام‌گذاری شده است.

این قضیه به بررسی روابط بین اضلاع مثلث‌های قائم‌الزاویه می‌پردازد و به‌طور خاص بیان می‌کند که در هر مثلث قائم‌الزاویه، مربع طول وتر (ضلع مقابل زاویه قائم) برابر با مجموع مربع‌های طول دو ضلع دیگر (اضلاع مجاور زاویه قائم) است. به عبارت ریاضی، این قضیه به صورت زیر بیان می‌شود:

c2=a2+b2 c^2 = a^2 + b^2

که در آن:

• c c طول وتر (ضلع بزرگتر)
• a a و b b طول دو ضلع دیگر (اضلاع مجاور به زاویه قائم) هستند.

این مقاله را هم بخوانید:  زندگی‌نامه کامل لوکوربوزیه مهم‌ترین معمار عصر مدرن

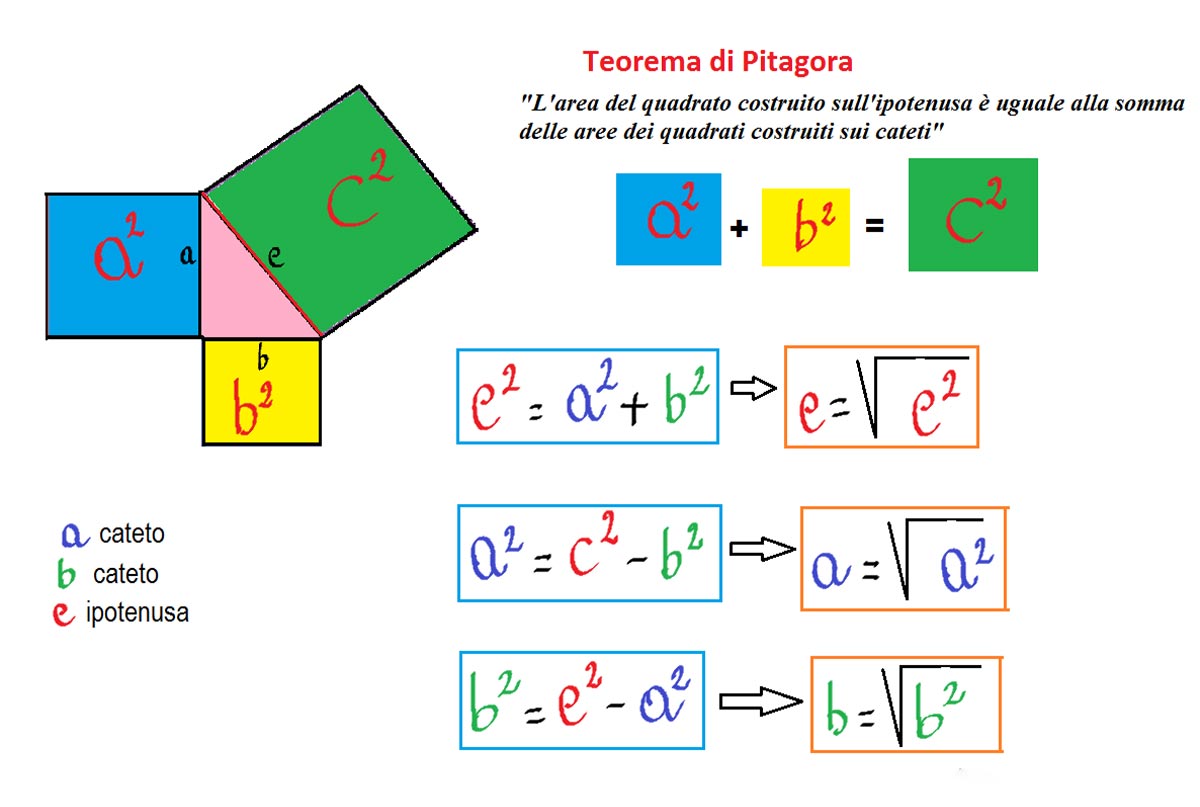
توضیح قضیه

این رابطه نشان می‌دهد که اگر طول‌های اضلاع یک مثلث قائم‌الزاویه را بدانیم، می‌توانیم طول ضلع سوم را محاسبه کنیم. به عنوان مثال، اگر طول‌های دو ضلع مجاور یک مثلث قائم‌الزاویه به ترتیب 3 و 4 واحد باشند، می‌توانیم با استفاده از قضیه فیثاغورس طول وتر را محاسبه کنیم:

c2=32+42c2=9+16c2=25c=5 c^2 = 3^2 + 4^2 \\ c^2 = 9 + 16 \\ c^2 = 25 \\ c = 5

بنابراین، طول وتر این مثلث 5 واحد است.

تاریخچه و اثبات

قضیه فیثاغورس یکی از نخستین قضایای ریاضی است که در تاریخ ثبت شده است و به دلیل سادگی و کاربرد گسترده‌اش، در بسیاری از فرهنگ‌ها و تمدن‌ها شناخته شده بود.هند، چین و بابل از جمله مکان‌هایی بودند که ریاضیدانان آن‌ها به نوعی از این قضیه آگاهی داشتند.

یکی از ساده‌ترین و مشهورترین روش‌های اثبات، استفاده از مربع‌ها بر روی اضلاع مثلث قائم‌الزاویه است. در این روش، می‌توان با ترسیم مربع‌هایی به ابعاد طول هر ضلع، نشان داد که مساحت مربع وتر برابر با مجموع مساحت مربع‌های دیگر اضلاع است. این رویکرد به وضوح نشان‌دهنده این است که چگونه ریاضیدانان قدیم به شناخت عمیقی از هندسه و روابط فضایی دست یافته بودند.

زندگی‌نامه دیگر افراد موفق: اگر به مطالعه زندگی‌نامه افراد موفق علاقه دارید توصیه می‌کنیم مقالات رومن آبراموویچ، بنجامین فرانکلین، فاطمه دانشور و فلورانس اسکاول شین را در رسانۀ دانشگاه کسب و کار بخوانید.

کاربردهای قضیه فیثاغورس

قضیه فیثاغورس در زمینه‌های مختلف علمی و عملی کاربردهای فراوانی دارد. در ادامه به برخی از این کاربردها اشاره خواهیم کرد:

اندازه‌گیری فاصله بین دو نقطه با استفاده از فاصله اقلیدسی

قضیه فیثاغورس به عنوان ابزاری مؤثر در محاسبه فاصله اقلیدسی بین دو نقطه در صفحه یا فضای سه‌بعدی به کار می‌رود. فاصله اقلیدسی بین دو نقطه، طول خطی است که این دو نقطه را به هم متصل می‌کند.

برای مثال، اگر دو نقطه A(x1,y1) A(x_1, y_1) و B(x2,y2) B(x_2, y_2) در صفحه داشته باشیم، فاصله اقلیدسی بین آن‌ها را می‌توان با استفاده از قضیه فیثاغورس به صورت زیر محاسبه کرد:

d=(x2−x1)2+(y2−y1)2 d = \sqrt{(x_2 – x_1)^2 + (y_2 – y_1)^2}

در این معادله، d d فاصله اقلیدسی بین A A و B B است. همان‌طور که مشاهده می‌شود، دو نقطه A A و B B یک مثلث قائم‌الزاویه با ضلع‌های x2−x1 x_2 – x_1 و y2−y1 y_2 – y_1 و هیپوتنوز d d تشکیل می‌دهند.

تعمیم به فضای سه‌بعدی

این روش را می‌توان به فضای سه‌بعدی نیز تعمیم داد. اگر دو نقطه A(x1,y1,z1) A(x_1, y_1, z_1) و B(x2,y2,z2) B(x_2, y_2, z_2) در فضا داشته باشیم، فاصله اقلیدسی بین آن‌ها را می‌توان با استفاده از قضیه فیثاغورس به صورت زیر محاسبه کرد:

d=(x2−x1)2+(y2−y1)2+(z2−z1)2 d = \sqrt{(x_2 – x_1)^2 + (y_2 – y_1)^2 + (z_2 – z_1)^2}

در این معادله، d d فاصله اقلیدسی بین A A و B B است. در اینجا نیز، می‌توانیم با توجه به ابعاد مختلف، فاصله بین دو نقطه را بر اساس اندازه‌گیری‌های ساده هندسی محاسبه کنیم.

این مقاله را هم بخوانید:  زندگی‌نامه کامل ژول ورن + قصه‌های جالب از داستان زندگی او

کاربردهای عملی

قضیه فیثاغورس در بسیاری از زمینه‌های علمی و مهندسی به کار می‌رود. برخی از این کاربردها عبارتند از:

• معماری و مهندسی: برای تعیین ابعاد و بررسی استحکام سازه‌ها.
• جغرافیا و نقشه‌برداری: برای محاسبه فاصله بین نقاط و ایجاد نقشه‌ها.
• فیزیک: در تحلیل نیروها و حرکت اجسام.
• رباتیک: برای تعیین موقعیت و حرکت ربات‌ها و ماشین‌ها.
• ماشین بینایی: در تحلیل تصاویر و تشخیص اشیاء.

قضیه فیثاغورس پایه‌ی هندسه اقلیدسی

قضیه فیثاغورس نه تنها یک قانون ریاضی است، بلکه یک ابزار حیاتی برای درک روابط فضایی و هندسی در دنیای واقعی به شمار می‌آید. این قضیه به عنوان یکی از پایه‌های هندسه اقلیدسی شناخته می‌شود و تأثیرات آن در تاریخ علم و ریاضیات غیرقابل انکار است. امروزه، این قضیه به طور گسترده در آموزش ریاضیات تدریس می‌شود و به دانش‌آموزان و دانشجویان کمک می‌کند تا مفاهیم پایه‌ای هندسه را بهتر درک کنند.

در نهایت، می‌توان گفت که قضیه فیثاغورس یک ابزار مفید و قدرتمند برای اندازه‌گیری فاصله بین دو نقطه در صفحه یا فضا با استفاده از فاصله اقلیدسی است. این کاربرد در بسیاری از زمینه‌های علمی و مهندسی مانند هندسه، فیزیک، رباتیک، ماشین بینایی، محاسبات مکانی و غیره به کار می‌رود. قضیه فیثاغورس نه تنها به عنوان یک اصل بنیادی در ریاضیات بلکه به عنوان یک ستون فقرات در بسیاری از علوم دیگر عمل می‌کند و به ما این امکان را می‌دهد که دنیای خود را بهتر بشناسیم و درک کنیم.